用 Python 解开恶魔拼图 Puzzle of Evil
被 恶魔拼图(Puzzle of Evil) 困住了一天之后,我决定上网搜索一下,我怀疑是否存在答案,于是就看到了这篇文章:
How wooden puzzles can destroy dev teams ,
不同的是他们找到了 Easy 难度的答案,只是解不出 Hard 难度。
好吧,看来 Easy 还是没问题的,是有答案的,那我也干脆用计算机暴力求解一下吧。
问题分解
拼图的外观如下:
两种难度的底板
参考 John Sullivan 的解法,用大三角形把两种难度框起来,从上到下,从左到右标上坐标。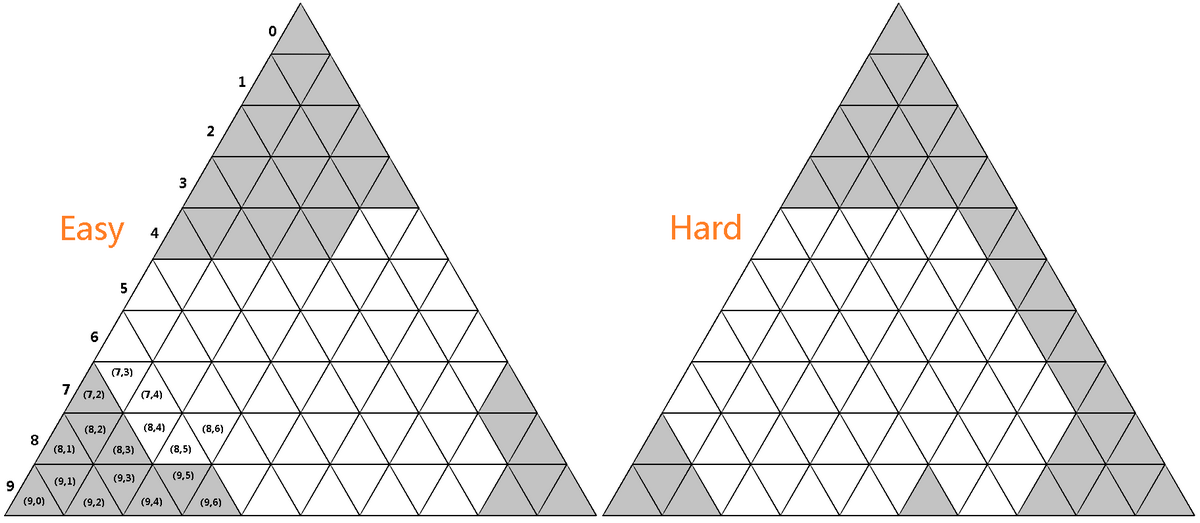
四个板块
虽然也是上过博士课程的人,但我的数学知识基本都还给老师了,干脆用最简单的方法来解决板块的旋转和翻面时的坐标变换难题。
每个板块有 2 面,按照形状有 6 个旋转的角度,因此有 12 个初始摆放位置(从大三角形的左下角开始),如下图:



求解过程
问题简化之后,剩下的就是循环求解,把每个板块先向右一格一格的移动,移到最右边,然后向上移动一格后,再依次从左向右移动,直到最上端。
移动的过程中,任何时候板块的任何部分都不能移出大三角形之外;每移动一格都通过板块上每个小三角形的坐标来判断是否整个板块都位于底板内,计算的结果列表如下:
| 板块 | A | B | C | D |
|---|---|---|---|---|
| 01 | 5 | 7 | 6 | 7 |
| 02 | 4 | 4 | 4 | 5 |
| 03 | 6 | 2 | 3 | 9 |
| 04 | 8 | 7 | 7 | 6 |
| 05 | 4 | 4 | 2 | 5 |
| 06 | 7 | 1 | 4 | 9 |
| 11 | 7 | 5 | 7 | 8 |
| 12 | 5 | 2 | 3 | 4 |
| 13 | 5 | 5 | 3 | 7 |
| 14 | 6 | 4 | 6 | 7 |
| 15 | 6 | 1 | 2 | 4 |
| 16 | 3 | 6 | 3 | 7 |
| 合计 | 66 | 48 | 50 | 78 |
一共 4 种板块,每个板块 0 开头有 1~6 六个角度,分别是 01~06,翻面之后为 11~16。
A 板块有 66 种可用摆放位置,B 板块有 48 种,为了减少循环的层数,先计算 A 和 B 板块同时摆放的可用位置,一共是 310 种。同理,C 和 D 板块有 539 种。
最后再把 AB 与 CD 的结果做一次循环,铛~铛~铛~铛~~~,不到一秒钟,结果出来了,唯一的一个答案。
按照板块上的坐标,先在大三角形里面标出了 A 板块的位置,答案如下:
- 想挑战解谜的朋友不要点开看:A 板块的放置位置图片 boardEasyAns.png
知道了 A 板块的位置之后,只剩下 3 个板块,难度下降很多,很快就解出来了,哦耶~~~
Hard 难度
Hard 难度和 Easy 难度的求解差别只在于底板形状的变化,因此只需要修改底板坐标参数即可。一番计算下来,结果果然为 0。
posA= 72
posB= 52
posC= 60
posD= 88
pos(A+B) = 354
pos(C+D) = 899
pos(A+B+C+D) = 0这和本文开头的那篇文章( How wooden puzzles can destroy dev teams )中说的一样,见下面的引用:
The hard side of the puzzle was
unsolvable.
Clearly there was a very evil puzzle master in our ranks.Jamie Wong readily admitted to bringing in the puzzle, but despite the staggering proof to the contrary, he was adamant that a solution existed. He said our solvers all shared a fatal flaw.
原文说,上面的算法存在一个致命的缺点,这么一说我就明白了,是这样的:
因为一开始我们就假设板块和底板都是有很多小三角形组成的,而且板块放置的时候是和底板中的小三角形重合的,Easy 难度也验证了这个假设;可是对于 Hard 难度,既然计算的结果为零,那就表明板块的放置不是和底板的小三角形重合。
基于这个推测,我试着先在底板外把 4 块拼图拼成一个紧凑的图案,结果居然让我一次成功,拼好之后移到底板中,空间绰绰有余。
最后的拼图结果就不放出来了,知道了上面的推测,答案就不远了。
Python 求解代码
我比较喜欢用 Jupyter Lab 编写一些简单的 Python 代码,编程全是自学的,欢迎大咖指教。
# Puzzle of Evil Solution
# 用大三角形板块包围底板形状
# 一个 4 个板块,每个板块有 6 个旋转角度和正反两面,以大三角形左下角为放置点,每个板块有 12 个初始位置,选择移动时位于底板内的那些位置保存成板块坐标
#
import numpy
# 三角形底板坐标初始化
RCord = numpy.zeros([10,19])
for i in range(9):
RCord[9][i+7] = 1
for i in range(12):
RCord[8][i+4] = 1
for i in range(13):
RCord[7][i+3] = 1
for i in range(13):
RCord[6][i+3] = 1
for i in range(11):
RCord[5][i+4] = 1
for i in range(3):
RCord[4][i+11] = 1
# print(RCord)
#[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
# [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
# [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
# [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
# [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 0. 0. 0. 0. 0.]
# [0. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0. 0.]
# [0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0.]
# [0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0.]
# [0. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0.]
# [0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0.]]
# 从大三角形左下角开始,向右向上依次移动一格,找寻每个板块的位于底板的可用位置,并附加到总数组中,返回可用的位置数
# array - 板块在大三角形左下角的坐标
# x - 板块可以向右移动的格数
# y - 板块可以向上移动的格数
# sjx - 每个板块有多少个三角形构成
# sumArr - 该板块所有的可用位置数组
# rightPos - 可以放在底板中的位置数
def sumPos(array,x,y,sjx,sumposArray):
rightPos = 0
for yy in range(y):
for xx in range(x-yy):
Temp = []
for m in range(sjx):
Temp.append([1,1])
for i in range(sjx):
Temp[i][0] = array[i][0] - yy
Temp[i][1] = array[i][1] + 2 * xx + yy
# print(Temp01)
sum = 0
for i in range(sjx):
sum = sum + RCord[Temp[i][0]][Temp[i][1]]
if sum == sjx:
rightPos+=1
# print(Temp01)
sumposArray.append(Temp)
return rightPos
# A 有 13 个小正三角形组成
posA = []
A01 = [[9,1],[8,1],[8,2],[7,2],[7,3],[7,4],[7,5],[7,6],[7,7],[7,8],[8,7],[8,8],[6,5]]
A02 = [[9,5],[9,6],[8,4],[8,5],[7,4],[7,5],[6,4],[6,5],[6,6],[6,8],[5,6],[5,7],[5,8]]
A03 = [[9,5],[9,6],[9,7],[9,8],[9,9],[8,3],[8,4],[8,5],[7,3],[7,4],[6,3],[6,4],[6,5]]
A04 = [[9,5],[8,2],[8,3],[8,4],[8,5],[8,6],[8,7],[8,8],[7,2],[7,3],[7,8],[7,9],[6,9]]
A05 = [[9,3],[9,4],[9,5],[8,3],[8,5],[8,6],[8,7],[7,6],[7,7],[6,6],[6,7],[5,5],[5,6]]
A06 = [[9,7],[9,8],[9,9],[8,8],[8,9],[7,7],[7,8],[7,9],[6,3],[6,4],[6,5],[6,6],[6,7]]
A11 = [[9,9],[8,2],[8,3],[8,8],[8,9],[7,2],[7,3],[7,4],[7,5],[7,6],[7,7],[7,8],[6,5]]
A12 = [[9,3],[9,4],[9,5],[8,3],[8,4],[7,3],[7,4],[7,5],[6,5],[6,6],[6,7],[6,8],[6,9]]
A13 = [[9,5],[9,6],[9,7],[8,3],[8,4],[8,5],[8,7],[7,3],[7,4],[6,3],[6,4],[5,4],[5,5]]
A14 = [[9,7],[8,4],[8,5],[8,6],[8,7],[8,8],[8,9],[8,10],[7,3],[7,4],[7,9],[7,10],[6,3]]
A15 = [[9,1],[9,2],[9,3],[9,4],[9,5],[8,5],[8,6],[8,7],[7,6],[7,7],[6,5],[6,6],[6,7]]
A16 = [[9,6],[9,7],[8,7],[8,8],[7,7],[7,8],[6,4],[6,6],[6,7],[6,8],[5,4],[5,5],[5,6]]
print('A01:', sumPos(A01,5,5,13,posA))# A01: x=5 y=5 A01: 5
print('A02:', sumPos(A02,4,3,13,posA))# A02: x=4 y=3 A02: 4
print('A03:', sumPos(A03,4,4,13,posA))# A03: x=4 y=3 A03: 6
print('A04:', sumPos(A04,4,3,13,posA))# A04: x=4 y=3 A04: 8
print('A05:', sumPos(A05,5,4,13,posA))# A05: x=5 y=4 A05: 4
print('A06:', sumPos(A06,4,3,13,posA))# A06: x=4 y=3 A06: 7
print('A11:', sumPos(A11,5,4,13,posA))# A11: x=5 y=4 A11: 7
print('A12:', sumPos(A12,4,4,13,posA))# A12: x=4 y=4 A12: 5
print('A13:', sumPos(A13,5,5,13,posA))# A13: x=5 y=5 A13: 5
print('A14:', sumPos(A14,4,4,13,posA))# A14: x=4 y=4 A14: 6
print('A15:', sumPos(A15,5,5,13,posA))# A15: x=5 y=5 A15: 6
print('A16:', sumPos(A16,4,4,13,posA))# A16: x=4 y=4 A16: 3
print('posA=',len(posA)) # lenA= 66
# B 有 12 个小正三角形组成
posB = []
B01 = [[9,7],[9,8],[9,9],[9,10],[8,2],[8,6],[8,7],[7,2],[7,3],[7,4],[7,5],[7,6]]
B02 = [[9,1],[9,2],[8,1],[8,2],[7,2],[7,3],[7,4],[7,5],[7,6],[7,7],[6,7],[6,8]]
B03 = [[9,5],[9,6],[9,7],[8,4],[8,5],[7,4],[7,5],[6,5],[6,6],[5,5],[5,6],[4,5]]
B04 = [[9,7],[9,8],[9,9],[9,10],[9,11],[8,6],[8,7],[8,11],[7,3],[7,4],[7,5],[7,6]]
B05 = [[9,0],[9,1],[8,1],[8,2],[8,3],[8,4],[8,5],[8,6],[7,6],[7,7],[6,6],[6,7]]
B06 = [[9,7],[8,6],[8,7],[7,6],[7,7],[6,7],[6,8],[5,7],[5,8],[4,5],[4,6],[4,7]]
B11 = [[9,1],[9,2],[9,3],[9,4],[9,5],[8,1],[8,5],[8,6],[7,6],[7,7],[7,8],[7,9]]
B12 = [[9,3],[9,4],[9,5],[8,5],[8,6],[7,5],[7,6],[6,4],[6,5],[5,4],[5,5],[4,5]]
B13 = [[9,10],[9,11],[8,10],[8,11],[7,5],[7,6],[7,7],[7,8],[7,9],[7,10],[6,4],[6,5]]
B14 = [[9,0],[9,1],[9,2],[9,3],[8,3],[8,4],[8,8],[7,4],[7,5],[7,6],[7,7],[7,8]]
B15 = [[9,5],[8,5],[8,6],[7,5],[7,6],[6,4],[6,5],[5,4],[5,5],[4,5],[4,6],[4,7]]
B16 = [[9,9],[9,10],[8,4],[8,5],[8,6],[8,7],[8,8],[8,9],[7,3],[7,4],[6,3],[6,4]]
print('B01:', sumPos(B01,5,5,12,posB)) # B01: x = 5, y = 5 B01: 7
print('B02:', sumPos(B02,4,4,12,posB)) # B02: x = 4, y = 4 B02: 4
print('B03:', sumPos(B03,5,5,12,posB)) # B03: x = 5, y = 5 B03: 2
print('B04:', sumPos(B04,4,4,12,posB)) # B04: x = 4, y = 4 B04: 7
print('B05:', sumPos(B05,5,5,12,posB)) # B05: x = 5, y = 5 B05: 4
print('B06:', sumPos(B06,4,4,12,posB)) # B06: x = 4, y = 4 B06: 1
print('B11:', sumPos(B11,4,4,12,posB)) # B11: x = 4, y = 4 B11: 5
print('B12:', sumPos(B12,5,5,12,posB)) # B12: x = 5, y = 5 B12: 2
print('B13:', sumPos(B13,4,4,12,posB)) # B13: x = 4, y = 4 B13: 5
print('B14:', sumPos(B14,5,5,12,posB)) # B14: x = 5, y = 5 B14: 4
print('B15:', sumPos(B15,4,4,12,posB)) # B15: x = 4, y = 4 B15: 1
print('B16:', sumPos(B16,5,5,12,posB)) # B16: x = 5, y = 5 B16: 6
print('posB=',len(posB)) # lenB= 48
# C 有 13 个小正三角形组成
posC = []
C01 = [[9,3],[9,4],[9,5],[9,6],[9,7],[9,8],[9,9],[8,2],[8,3],[8,9],[8,10],[7,2],[7,3]]
C02 = [[9,1],[9,2],[9,3],[9,4],[9,5],[8,1],[8,5],[8,6],[7,6],[7,7],[6,6],[6,7],[5,6]]
C03 = [[9,7],[9,8],[9,9],[8,9],[8,10],[7,9],[7,10],[6,8],[6,9],[5,5],[5,6],[5,7],[5,8]]
C04 = [[9,8],[9,9],[8,1],[8,2],[8,8],[8,9],[7,2],[7,3],[7,4],[7,5],[7,6],[7,7],[7,8]]
C05 = [[9,3],[8,2],[8,3],[7,2],[7,3],[6,3],[6,4],[6,8],[5,4],[5,5],[5,6],[5,7],[5,8]]
C06 = [[9,5],[9,6],[9,7],[9,8],[8,4],[8,5],[7,3],[7,4],[6,3],[6,4],[5,4],[5,5],[5,6]]
C11 = [[9,3],[9,4],[9,5],[9,6],[9,7],[9,8],[9,9],[8,2],[8,3],[8,9],[8,10],[7,9],[7,10]]
C12 = [[9,2],[9,3],[9,4],[9,5],[8,5],[8,6],[7,6],[7,7],[6,6],[6,7],[5,4],[5,5],[5,6]]
C13 = [[9,9],[8,9],[8,10],[7,9],[7,10],[6,4],[6,8],[6,9],[5,4],[5,5],[5,6],[5,7],[5,8]]
C14 = [[9,1],[9,2],[8,1],[8,2],[8,8],[8,9],[7,2],[7,3],[7,4],[7,5],[7,6],[7,7],[7,8]]
C15 = [[9,3],[9,4],[9,5],[8,2],[8,3],[7,2],[7,3],[6,3],[6,4],[5,4],[5,5],[5,6],[5,7]]
C16 = [[9,5],[9,6],[9,7],[9,8],[9,9],[8,4],[8,5],[8,9],[7,3],[7,4],[6,3],[6,4],[5,4]]
print('C01:', sumPos(C01,4,4,13,posC)) # C01: x=4 y=4 C01: 6
print('C02:', sumPos(C02,5,5,13,posC)) # C02: x=5 y=5 C02: 4
print('C03:', sumPos(C03,4,4,13,posC)) # C03: x=4 y=4 C03: 3
print('C04:', sumPos(C04,5,5,13,posC)) # C04: x=5 y=5 C04: 7
print('C05:', sumPos(C05,4,4,13,posC)) # C05: x=4 y=4 C05: 2
print('C06:', sumPos(C06,5,5,13,posC)) # C06: x=5 y=5 C06: 4
print('C11:', sumPos(C11,4,4,13,posC)) # C11: x=4 y=4 C11: 7
print('C12:', sumPos(C12,5,5,13,posC)) # C12: x=5 y=5 C12: 3
print('C13:', sumPos(C13,4,4,13,posC)) # C13: x=4 y=4 C13: 3
print('C14:', sumPos(C14,5,5,13,posC)) # C14: x=5 y=5 C14: 6
print('C15:', sumPos(C15,4,4,13,posC)) # C15: x=4 y=4 C15: 2
print('C16:', sumPos(C16,5,5,13,posC)) # C16: x=5 y=5 C16: 3
print('posC=',len(posC)) # lenC= 50
# D 有 11 个小正三角形组成
posD = []
D01 = [[9,1],[9,3],[8,1],[8,2],[8,3],[8,4],[8,5],[8,6],[7,6],[7,7],[6,7]]
D02 = [[9,5],[9,6],[8,5],[8,6],[8,7],[7,6],[7,7],[6,6],[6,7],[5,5],[5,6]]
D03 = [[9,7],[9,8],[9,9],[8,6],[8,7],[8,8],[7,2],[7,3],[7,4],[7,5],[7,6]]
D04 = [[9,1],[8,1],[8,2],[7,2],[7,3],[7,4],[7,5],[7,6],[7,7],[6,5],[6,7]]
D05 = [[9,5],[9,6],[8,4],[8,5],[7,4],[7,5],[6,4],[6,5],[6,6],[5,5],[5,6]]
D06 = [[9,5],[9,6],[9,7],[9,8],[9,9],[8,3],[8,4],[8,5],[7,2],[7,3],[7,4]]
D11 = [[9,1],[9,2],[9,3],[9,4],[9,5],[8,5],[8,6],[8,7],[7,6],[7,7],[7,8]]
D12 = [[9,4],[9,5],[8,5],[8,6],[7,5],[7,6],[6,4],[6,5],[6,6],[5,4],[5,5]]
D13 = [[9,9],[8,8],[8,9],[7,3],[7,4],[7,5],[7,6],[7,7],[7,8],[6,3],[6,5]]
D14 = [[9,1],[9,2],[9,3],[8,2],[8,3],[8,4],[7,4],[7,5],[7,6],[7,7],[7,8]]
D15 = [[9,4],[9,5],[8,3],[8,4],[8,5],[7,3],[7,4],[6,3],[6,4],[5,4],[5,5]]
D16 = [[9,7],[9,9],[8,4],[8,5],[8,6],[8,7],[8,8],[8,9],[7,3],[7,4],[6,3]]
print('D01:', sumPos(D01,5,5,11,posD)) # D01: x=5 y=5 D01: 7
print('D02:', sumPos(D02,5,5,11,posD)) # D02: x=5 y=5 D02: 5
print('D03:', sumPos(D03,5,5,11,posD)) # D03: x=5 y=5 D03: 9
print('D04:', sumPos(D04,5,5,11,posD)) # D04: x=5 y=5 D04: 6
print('D05:', sumPos(D05,5,5,11,posD)) # D05: x=5 y=5 D05: 5
print('D06:', sumPos(D06,5,5,11,posD)) # D06: x=5 y=5 D06: 9
print('D11:', sumPos(D11,5,5,11,posD)) # D11: x=5 y=5 D11: 8
print('D12:', sumPos(D12,5,5,11,posD)) # D12: x=5 y=5 D12: 4
print('D13:', sumPos(D13,5,5,11,posD)) # D13: x=5 y=5 D13: 7
print('D14:', sumPos(D14,5,5,11,posD)) # D14: x=5 y=5 D14: 7
print('D15:', sumPos(D15,5,5,11,posD)) # D15: x=5 y=5 D15: 4
print('D16:', sumPos(D16,5,5,11,posD)) # D16: x=5 y=5 D16: 7
print('posD=',len(posD)) # lenD= 78
# 找出同时放置 A、B 板块中可用的位置
# 循环判断从 A、B 中选取的位置是否有重复的坐标,没有重复坐标则视为可以同时放置 AB(可用的位置)
posAB = []
for a in posA:
for b in posB:
tmp = [var for var in a if var in b]
if len(tmp) == 0:
posAB.append(a+b)
print('pos(A+B) = ',len(posAB))
# 找出同时放置 C、D 板块中可用的位置
# 循环判断从 C、D 中选取的位置是否有重复的坐标,没有重复坐标则视为可以同时放置 CD(可用的位置)
posCD = []
for c in posC:
for d in posD:
tmp = [var for var in c if var in d]
if len(tmp) == 0:
posCD.append(c+d)
print('pos(C+D) = ',len(posCD))
# 找出同时放置 A、B、C、D 板块中可用的位置
poseABCD = []
for ab in posAB:
for cd in posCD:
tmp = [var for var in ab if var in cd]
if len(tmp) == 0:
poseABCD.append(ab+cd)
print('pos(A+B+C+D) = ',len(poseABCD))
print(poseABCD)
#[[[9, 9], [9, 10], [9, 11], [9, 12], [9, 13], [8, 13], [8, 14], [8, 15], [7, 14], [7, 15], [6, 13], [6, 14], [6, 15],
# [7, 5], [7, 6], [6, 5], [6, 6], [5, 6], [5, 7], [5, 8], [5, 9], [5, 10], [5, 11], [4, 11], [4, 12],
# [8, 4], [8, 5], [8, 6], [8, 7], [8, 8], [8, 9], [8, 10], [7, 3], [7, 4], [7, 10], [7, 11], [6, 3], [6, 4],
# [7, 7], [7, 9], [6, 7], [6, 8], [6, 9], [6, 10], [6, 11], [6, 12], [5, 12], [5, 13], [4, 13]]]