亲爱的同学，祝贺你迎来了义务教育阶段最后一个学期的数学学习生活！

一　直角三角形的边角关系

1、锐角三角函数

• 正切（tangent）：在 $Rt\triangle ABC$ 中，如果锐角 A 确定，那么 $\angle A$ 的对边与邻边的比便随之确定，这个比叫做 $\angle A$ 的正切，记作 tan A，即
  $tan A = \frac{\angle A 的对边}{\angle A 的邻边}$
• tan A 的值越大，梯子越陡。
• 正切也经常用来描述山坡的坡度。坡面的铅直高度与水平宽度的比称为坡度（或坡比）。
• 正弦（sine）：在 $Rt\triangle ABC$ 中，如果锐角 A 确定，那么 $\angle A$ 的对边与斜边的比便随之确定，这个比叫做 $\angle A$ 的正弦，记作 sin A，即
  $sin A = \frac{\angle A 的对边}{斜边}$
• 余弦（cosine）：在 $Rt\triangle ABC$ 中，如果锐角 A 确定，那么 $\angle A$ 的邻边与斜边的比便随之确定，这个比叫做 $\angle A$ 的余弦，记作 cos A，即
  $cos A = \frac{\angle A 的邻边}{斜边}$
• 三角函数（trigonometric function）
• sin A 的值越大，梯子越陡；cos A 的值越小，梯子越陡。

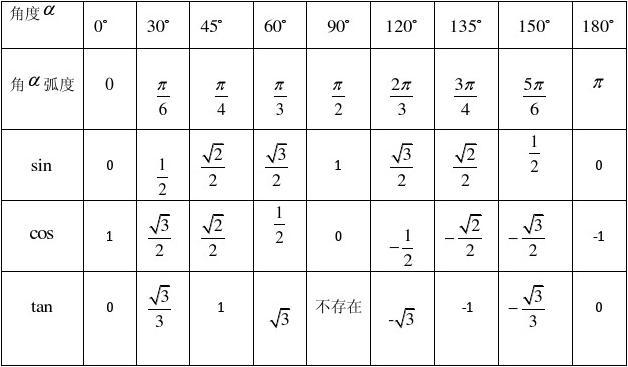
2、30°，45°，60° 角的三角函数值

3、三角函数的计算

• 用科学计算器求三角函数
• 已知三角函数值，反求角度

4、解直角三角形

• 解直角三角形：由直角三角形中已知的元素，求出所有未知元素的过程。
• 在直角三角形的 6 个元素中，直角是已知元素，如果再知道一条边和第三格元素，那么这个三角形的所有元素就都可以确定下来。

5、三角函数的应用
6、利用三角函数测高

二　二次函数

1、二次函数

• 二次函数（quadratic function）：一般地，若两个变量 x，y 之间的对应关系可以表示成 $y=ax^{2}+bx+c$（a，b，c 是常数，$a\neq 0$）的形式，则称 y 是 x 的二次函数。

2、二次函数的图像与性质

• 二次函数 $y=x^{2}$ 的图象是一条抛物线（parabola），它的开口向上，且关于 y 轴对称。对称轴与抛物线的交点是抛物线的顶点，它是图象的最低点。
• 一般地，平移二次函数 $y=ax^{2}$ 的图象便可得到二次函数 $y=a(x-h)^{2}+k$ 的图象。
  a > 0，开口向上，a < 0，开口向下；对称轴直线 x = h ；顶点坐标（h，k）
• 二次函数 $y=ax^{2}+bx+c$ 图象的对称轴是直线 $x=-\frac{b}{2a}$，顶点坐标是$(-\frac{b}{2a},\frac{4ac-b^{2}}{4a})$。

3、确定二次函数的表达式

• 通过图象经过的点来反推二次函数的各项系数，从而得到二次函数表达式

4、二次函数的应用
5、二次函数与一元一次方程

• 二次函数 $y=ax^{2}+bx+c$ 的图象与 x 轴的交点有三种情况：有两个交点、有一个交点、没有交点。
  与此相对应，一元二次方程 $ax^{2}+bx+c=0$ 的根也有三种情况：有两个不相等的实数根、有两个相等的实数根、没有实数根。
• 二次函数 $y=ax^{2}+bx+c$ 的图象与 x 轴交点的横坐标就是一元二次方程 $ax^{2}+bx+c=0$ 的根。

三　圆

1、圆

• 圆：平面上到定点的距离等于定长的所有点组成的图形。定点就是圆心，定长就是半径。
  以点 O 为圆心的圆记作 $\bigotimes O$，读作“圆 O”。
• 弦（chord）：连接圆上任意两点的线段
• 直径（diameter）：经过圆心的弦
• 圆弧：圆上任意两点间的部分。优弧、劣弧
• 半圆（semicircle）：圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做~
• 等圆（equal circles）：能够重合的两个圆
• 等弧（equal arcs）：在同圆或等圆中，能够互相重合的弧
• 点与圆的位置关系有三种：点在圆外、点在圆上、点在圆内。

2、圆的对称性

• 圆是轴对称图形，其对称轴是任意一条过圆心的直线。
• 圆是中心对称图形，对称中心为圆心。
• 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。
• 在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

*3、垂径定理

• 垂径定理：垂直于弦的直径平分这条弦，并且平方弦所对的弧。
• 平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧。

4、圆周角和圆心角的关系

• 圆周角（angle of circumference）：顶点在圆上，两边分别与圆还有交点
• 圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的一半。
• 推论：同弧或等弧所对的圆周角相等。
• 推论：直径所对的圆周角是直角；90°的圆周角所对的弦是直径。
• 圆内接四边形（inscribed quadrilateral）：四边形 ABCD 的四个顶点都在圆上，这个圆叫做四边形的外接圆。
• 推论：圆内接四边形的对角互补。

5、确定圆的条件

• 尺规作过不在同一条直线上的三点的圆
• 不在同一条直线上的三个点确定一个圆。
• 三角形的外接圆（circumcircle of triangle）：三角形的三个顶点确定一个圆
• 外心（circumcenter）：外接圆的圆心是三角形三边垂直平分线的交点

6、直线和圆的位置关系

• 直线和圆有三种关系：相交、相切和相离。
• 圆的切线（tangent line）：直线和圆有唯一的公共点（即直线和圆相切）时，这条直线叫做~，这个唯一的公共点叫做切点（point of tangency）。
• 圆的切线垂直于过切点的半径。
• 过半径外端且垂直于这条半径的直线是圆的切线。
• 三角形的内切圆（inscribed circle of triangle）：和三角形三边都相切的圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心（incenter）。

*7、切线长定理

• 切线长（length of the tangent）：过圆外一点画圆的切线，这点和切线之间的线段长叫做这点到圆的~
• 切线长定理：过圆外一点画圆的两条切线，它们的切线长相等。

8、圆内接正多边形

• 圆内接正多边形：顶点都在同一圆上的正多边形，这个圆叫做该正多边形的外接圆。
• 边心距：正多边形的中心到边的距离
• 尺规作正五边形

9、弧长及扇形的面积

• 在半径为 R 的圆中，n° 的圆心角所对的弧长（arc length）的计算公式为 $l=\frac{n}{180}\pi R$。
• 如果扇形的半径为 R，圆心角为 n°，那么扇形面积的计算公式为$S_{扇形}=l\cdot \frac{R}{2}$，也等于$$S_{扇形}=\frac{n}{360}\pi R^{2}$$

综合与实践

• 视力的变化
• 哪种方式更合算
• 设计遮阳篷