人教版高中数学必修第一册A版知识要点
为啥深圳义务教育阶段的数学使用的是北师大的版本,到了高中就换成人教版了,一开始就用人教版不好吗?
第一章 集合与常用逻辑用语
1.1 集合的概念
- 元素(element):一般地,我们把研究对象统称为~
- 集合(set):一些元素组成的总体叫做~,简称为集。
- 给定的集合,它的元素必须是确定的,集合中的元素是不重复出现的,元素在集合中是无序的。
- 集合相等:构成两个集合的元素是一样的
- 如果 a 是集合 A 的元素,就说 a 属于(belong to)集合 A,记作 $a \in A$;
如果 a 不是集合 A 中的元素,就说 a 不属于(not belong to)集合 A,记作 $a\notin A$。 - 自然数集 N、正整数集 $N^{\ast}或N_{+}$、整数集 Z、有理数集 Q、实数集 R
- 列举法:把集合的所有元素一一列举出来,并用花括号“{ }”括起来表示集合的方法。
- 描述法:一般地,设 A 是一个集合,我们把集合 A 中所有具有共同特征 P(x) 的元素 x 所组成的集合表示为 $\{x\in A|P(x)\}$,这种表示集合的方法称为~。
1.2 集合间的基本关系
- 子集(subset):一般地,对于两个集合 A,B,如果集合 A 中任意一个元素都是集合 B 中的元素,就称集合 A 为集合 B 的子集,
记作 $A\subseteq B$ 或 $B\supseteq A$,读作“A 包含于 B”或“B 包含 A”。 - Venn图:用平面上封闭曲线的内部代表集合的图形。
- 若 $A\subseteq B$ ,且 $B\subseteq A$,则 A = B。
- 真子集(proper subset):如果集合 $A\subseteq B$,但存在元素 $x \in B$,且 $x \notin A$,就称集合 A 是集合 B 的~,
记作A ⫋ B 或 B ⫌ A,读作“A 真包含于 B”或“B 真包含 A”。 - 空集(empty set):一般地,我们把不含任何元素的集合叫做~,记为 Ø,并规定:空集是任何集合的子集。
- 任何一个集合是它本身的子集,即 $A\subseteq A$;
对于集合 A,B,C,如果 $A\subseteq B$,且 $B\subseteq C$,那么 $A\subseteq C$。
1.3 集合的基本运算
- 并集(union set):一般地,由所有属于集合 A 或属于集合 B 的元素组成的集合,称为集合 A 与 B 的并集,
记作 $A\cup B$,读作“A 并 B”,即 $A\cup B$={x|$x \in A$,或 $x \in B$}。 - 交集(intersection set):一般地,由所有属于集合 A 且属于集合 B 的元素组成的集合,称为集合 A 与 B 的~,
记作 $A\cap B$,读作“A 交 B”,即 $A\cap B$={x|$x \in A$,且 $x \in B$}。 - 全集(universe set):一般地,如果一个集合含有所研究问题中涉及到所有元素,那么就称这个集合为~,通常记作 U。
- 补集(complementary set):对于一个集合 A,由全集 U 中不属于集合 A 的所有元素组成的集合称为集合 A 相对于全集 U 的补集,简称为集合 A 的补集,记作 C$_{U}A$,即 C$_{U}A$={x|$x \in U$,且 $x \notin A$}。
- 有限集:含有限个元素的集合,用 card(A)来表示有限集合 A 中元素的个数。
- 一般地,对任意两个有限集合 A,B,有 card($A\cup B$)= card(A)+card(B)- card($A\cap B$)
- 图解法解决复杂的交集、并集问题有明显的优越性。
1.4 充分条件与必要条件
1.4.1 充分条件与必要条件
- 一般地,“若 p,则 q”为真命题,是指由 p 通过推理可以得出 q。这时,我们就说,由 p 可以推出 q,记作 $p\Rightarrow q$,并且说,p 是 q 的充分条件(sufficient condition),q 是 p 的必要条件(necessary condition)。
如果“若 p,则 q”为假命题,那么由条件 p 不能推出结论 q,记作 p ⇏ q。此时,我们就说 p 不是 q 的充分条件,q 不是 p 的必要条件。 - 一般来说,对给定结论 q,使得 q 成立的条件 p 是不唯一的。
- 一般来说,给定条件 p,由 p 可以推出的结论 q 是不唯一的。
- 一般地,要判断“若 p,则 q”形式的命题中 q 是否为 p 的必要条件,只需判断是否有“$p\Rightarrow q$”,即“若 p,则 q”是否为真命题。
- 一般地,数学中的每一条判定定理都给出了相应数学结论成立的一个充分条件。
- 一般地,数学中的每一条性质定理都给出了相应数学结论成立的一个必要条件。
1.4.2 充要条件
- 如果“若 p,则 q”和它的逆命题“若 q,则 p”均是真命题,即既有 $p\Rightarrow q$,又有 $q\Rightarrow p$,就记作 $p\Leftrightarrow q$。此时,p 既是 q 的充分条件,也是 q 的必要条件,我们说 p 是 q 的充分必要条件,简称为充要条件(sufficient and necessary condition)。
1.5 全称量词与存在量词
1.5.1 全称量词与存在量词
- 短语“所有的”“任意一个”在逻辑中通常叫做全称量词(universal quantifier),并用符号“$\forall$”表示。含有全称量词的命题,叫做全称量词命题(universal proposition)。常见的全称量词还有“一切”“每一个”“任给”等。
全称量词命题“对 M 中任意一个 x,p(x)成立”,用符号简记为 $\forall x \in M, p(x)$。 - 短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词(existential quantifier),并用符号“$\exists$”表示。含有存在量词的命题,叫做存在量词命题(existential proposition)。
存在量词命题“存在 M 中的元素 x,p(x)成立”可用符号简记为 $\exists x\in M, p(x)$。
1.5.2 全程量词命题和存在量词命题的否定
- 全称量词命题:$\forall x \in M, p(x)$,它的否定:$\exists x\in M, ┐ p(x)$。
- 存在量词命题:$\exists x\in M, p(x)$,它的否定:$\forall x \in M, ┐ p(x)$。
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
- a > b ⇔ a - b > 0
- a = b ⇔ a - b = 0
- a < b ⇔ a - b < 0
- 一般地,$\forall a,b\in R$,有 $a^{2}+b^{2}\geqslant 2ab$,当且仅当 a = b 时,等号成立。
- 等式性质1:如果 a = b,那么 b = a;
等式性质2:如果 a = b, b = c,那么 a = c;
等式性质3:如果 a = b,那么 a ± c = b ± c;
等式性质4:如果 a = b,那么 ac = bc;
等式性质5:如果 a = b,c ≠ 0,那么 $\frac{a}{c}=\frac{b}{c}$. - 不等式性质1:如果 a > b,那么 b < a;如果 b < a,那么 a > b。即 a > b ⇔ b < a。
不等式性质2:如果 a > b, b > c, 那么 a > c。即 a > b, b > c ⇒ a > c。
不等式性质3:如果 a > b,那么 a + c > b + c。
不等式性质4:如果 a > b,c > 0,那么 ac > bc;如果 a > b,c < 0,那么 ac < bc。
不等式性质5:如果 a > b,c > d,那么 a + c > b + d。
不等式性质6:如果 a > b > 0,c > d > 0,那么 ac > bd。
不等式性质7:如果 a > b > 0,那么 $a^{n} > b^{n}(n\in N, n\geqslant 2)$。
2.2 基本不等式(basic inequality)
- 如果 a > 0,b > 0,可得 $\sqrt{ab}\leqslant \frac{a+b}{2}$,当且仅当 a = b 时,等号成立。
- $\sqrt{ab}$ 叫做正数 a,b 的几何平均数,$\frac{a+b}{2}$ 叫做正数 a,b 的算术平均数。
两个正数的算术平均数不小于它们的几何平均数。
2.3 二次函数与一元二次方程、不等式
- 一般地,我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式(quadric inequality in one unknown)。
一元二次不等式的一般形式是 $ax^{2}+bx+c>0$ 或 $ax^{2}+bx+c<0$,其中 a,b,c 均为常数,a ≠ 0。 - 一般地,对于二次函数 $y=ax^{2}+bx+c$,我们把使 $ax^{2}+bx+c=0$ 的实数 x 叫做二次函数 $y=ax^{2}+bx+c$ 的零点。

- 利用框图可以清晰地表示求解一元二次不等式的过程:
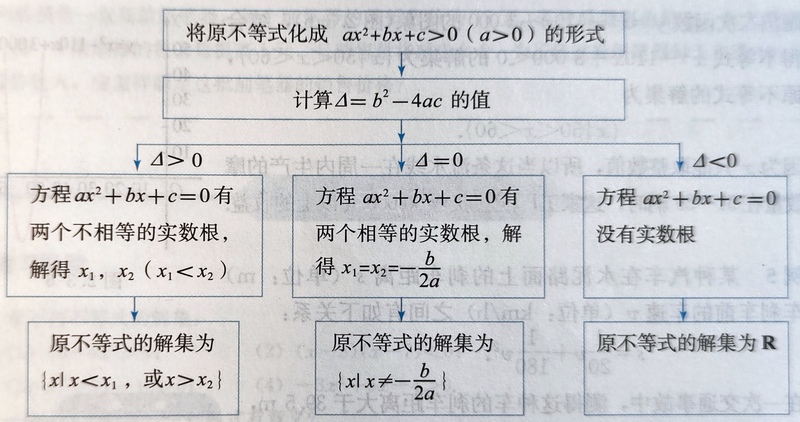
第三章 函数的概念与性质
3.1 函数的概念及其表示
3.1.1 函数的概念
- 一般地,设 A,B 是非空的实数集,如果对于集合 A 中的任意一个数 x,按照某种确定的对应关系 f,在集合 B 中都有唯一确定的数 y 和它对应,那么就称 f:A → B 为从集合 A 到集合 B 的一个函数(function),记作 $y=f(x), x\in A$。
其中,x 叫做自变量,x 的取值范围 A 叫做函数的定义域(domain);与 x 的值相对应的 y 值叫做函数值,函数值的集合{f(x)|$x\in A$} 叫做函数的值域(range)。 - 设 a,b 是两个实数,而且 a < b。我们规定:
(1)满足不等式 $a\leqslant x\leqslant b$ 的实数 x 的集合叫做闭区间,表示为 $[a,b]$;
(2)满足不等式 $a < x < b$ 的实数 x 的集合叫做开区间,表示为 (a,b);
(3)满足不等式 $a\leqslant x < b$ 或 $a < x\leqslant b$的实数 x 的集合叫做半开半闭区间,分别表示为 $[a,b),(a,b]$。
这里的实数 a 与 b 都叫做相应区间的端点。 - 在数轴表示时,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点。
- 实数集 R 可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”。
- 一个函数的构成要素为:定义域、对应关系和值域。
3.1.2 函数的表示法
- 解析法:用数学表达式表示两个变量之间的对应关系
- 列表法:列出表格来表示两个变量之间的对应关系
- 图象法:用图象表示两个变量之间的对应关系
- 分段函数:对于自变量 x 的不同的取值范围有不同的解析式的函数。
3.2 函数的基本性质
3.2.1 单调性与最大(小)值
- 函数的单调性:函数值随自变量的增大而增大(或减小)的性质
- 一般地,设函数 f(x)的定义域为 I,区间 $D\subseteq I$:
如果 $\forall x_{1},x_{2}\in D$,当 $x_{1}<x_{2}$ 时,都有 $f(x_{1})<f(x_{2})$,那么就称函数 f(x)在区间 D 上单调递增。
特别地,当函数 f(x)在它的定义域上单调递增时,我们就称它是增函数(increasing function)。
如果 $\forall x_{1},x_{2}\in D$,当 $x_{1}<x_{2}$ 时,都有 $f(x_{1})>f(x_{2})$,那么就称函数 f(x)在区间 D 上单调递减。
特别地,当函数 f(x)在它的定义域上单调递减时,我们就称它是减函数(decreasing function)。 - 如果函数 y=f(x)在区间 D 上单调递增或单调递减,那么就说函数 y=f(x)在这一区间具有(严格的)单调性,区间 D 叫做 y=f(x)的单调区间。
- 一般地,设函数 y=f(x)的定义域为 I,如果存在实数 M 满足:
(1)$\forall x\in I $,都有 $f(x)\leqslant M$;
(2)$\exists x_{0}\in I$,使得 $f(x_{0}) = M$
那么,我们称 M 是函数 y=f(x)的最大值(maximum value)。 - 最小值(minimum value)
3.2.2 奇偶性
- 一般地,设函数 f(x)的定义域为 I,如果 $\forall x\in I $,都有 $-x\in I$,且 f(-x)= f(x),那么函数 f(x)就叫做偶函数(even function)。
- 一般地,设函数 f(x)的定义域为 I,如果 $\forall x\in I $,都有 $-x\in I$,且 f(-x)= -f(x),那么函数 f(x)就叫做奇函数(odd function)。
- 奇偶性是函数在它的定义域上的整体性质,所以判断函数的奇偶性应先明确它的定义域。
3.3 幂函数
- 一般地,函数 $y=x^{a}$ 叫做幂函数(power function),其中 x 是自变量,a 是常数。
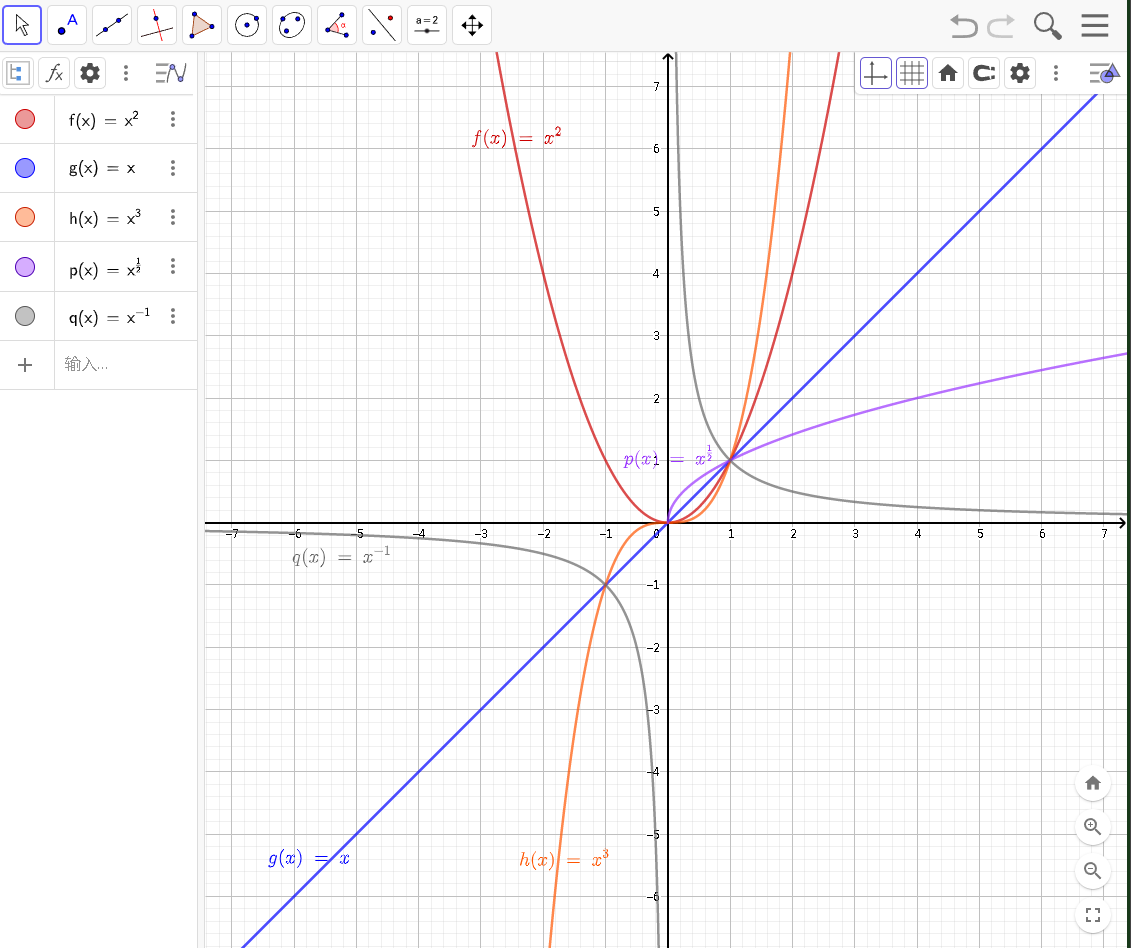
3.4 函数的应用(一)
第四章 指数函数与对数函数
4.1 指数
4.1.1 n 次方根与分数指数幂
- 一般地,如果 $x^{n}=a$,那么 x 叫做 a 的 n 次方根,其中 n > 1,且 $n\in N^{*}$。
- 负数没有偶次方根。0 的任何次方根都是 0,记作 $\sqrt[n]{0}=0$。
- 式子 $\sqrt[n]{a}$ 叫做根式(radical),这里 n 叫做根指数,a 叫做被开方数。
当 n 为奇数时,$\sqrt[n]{a^{n}}=a$;
当 n 为偶数时,$\sqrt[n]{a^{n}}=\left| a\right|=\left\{\begin{matrix}a,a\geqslant 0\\-a,a<0\end{matrix}\right.$ - 正数的正分数指数幂:$a^{\frac{m}{n}}=\sqrt[n]{a^{m}}(a>0,m,n\in N^{*},n>1)$
正数的负分数指数幂:$a^{-\frac{m}{n}}=\frac{1}{a^{\frac{m}{n}}}=\frac{1}{\sqrt[n]{a^{m}}}(a>0,m,n\in N^{*},n>1)$ - 0 的正分数指数幂等于 0,0 的负分数指数幂没有意义。
- 对于任意有理数 r,s,均有:
(1)$a^{r}a^{s}=a^{r+s}(a>0,r,s\in Q)$
(2)$(a^{r})^{s}=a^{rs}(a>0,r,s\in Q)$
(3)$(ab)^{r}=a^{r}b^{r}(a>0,b>0,r\in Q)$
4.1.2 无理数指数幂及其运算性质
- 一般地,无理数指数幂是一个确定的实数;实数指数幂是一个确定的实数。
- 对于任意实数 r,s,均有:
(1)$a^{r}a^{s}=a^{r+s}(a>0,r,s\in R)$
(2)$(a^{r})^{s}=a^{rs}(a>0,r,s\in R)$
(3)$(ab)^{r}=a^{r}b^{r}(a>0,b>0,r\in R)$
4.2 指数函数
4.2.1 指数函数的概念
- 增长量、增长率是刻画事物变化规律的两个很重要的量。增长率为常数的变化方式称为指数增长。
- 一般地,函数 $y=a^{x}(a>0,且a\neq 1)$ 叫做指数函数(exponential function),其中指数 x 是自变量,定义域是 R。
4.2.2 指数函数的图象和性质
- 底数互为倒数的两个指数函数的图象关于 y 轴对称。
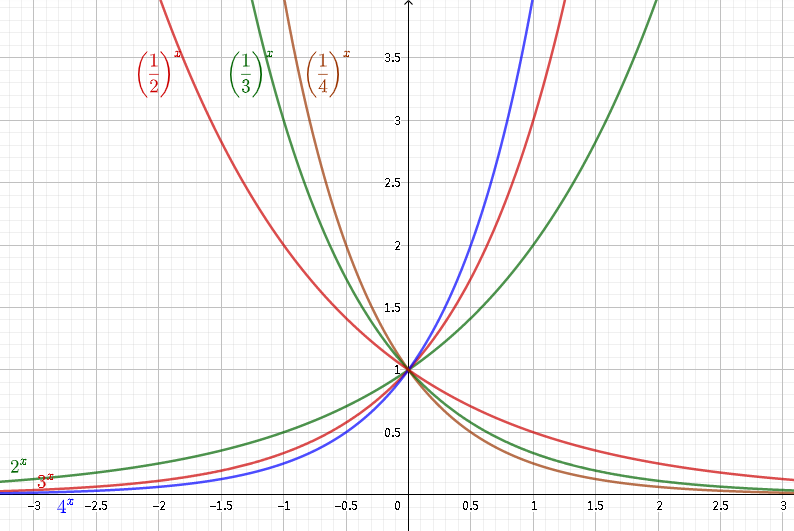
- 指数函数的图象和性质如下表:
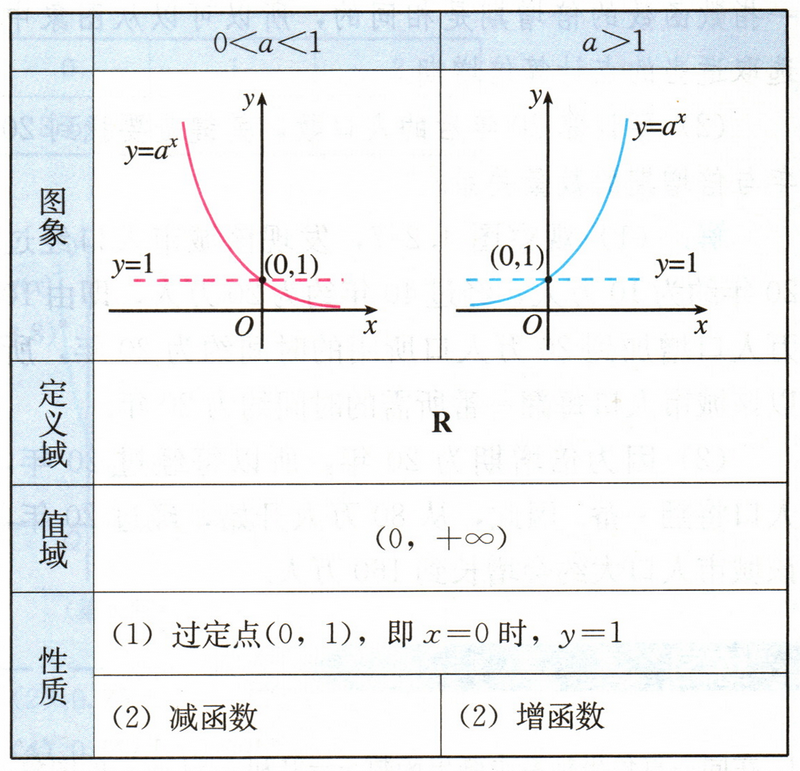
4.3 对数
4.3.1 对数的概念
- 一般地,如果 $a^{x}=N(a>0,且 a\neq 1)$,那么数 x 叫做以 a 为底 N 的对数(logarithm),记作 $x=log_{a}N$,其中 a 叫做对数的底数,N 叫做真数。
- 通常,我们将以 10 为底的对数叫做常用对数(common logrithm),并把 $log_{10}N$ 记为 lgN
以 e 为底的对数称为自然对数(natural logarithm),并把 $log_{e}N$ 记为 lnN - 对数与指数间的关系:当 a > 0,a ≠ 1 时,$a^{x}=N\Leftrightarrow x=log_{a}N$
负数和 0 没有对数;$log_{a}1=0,log_{a}a=1$
4.3.2 对数的运算
- 如果 a > 0,且 a ≠ 1,M > 0,N > 0,那么
(1)$log_{a}(MN)=log_{a}M+log_{a}N$
(2)$log_{a}\frac{M}{N}=log_{a}M-log_{a}N$
(3)$log_{a}M^{n}=nlog_{a}M(n\in R)$ - 对数换底公式:$log_{a}b=\frac{log_{c}b}{log_{c}a}(a>0, 且 a\neq 1;b>0;c>0, 且 c\neq 1)$
4.4 对数函数
4.4.1 对数函数的概念
- 一般地,函数 $y=log_{a}x(a>0, 且 a\neq 1)$ 叫做对数函数(logarithmic function),其中 x 是自变量,定义域是 (0,+∞)
4.4.2 对数函数的图象和性质
- 底数互为倒数的两个对数函数的图象关于 x 轴对称。
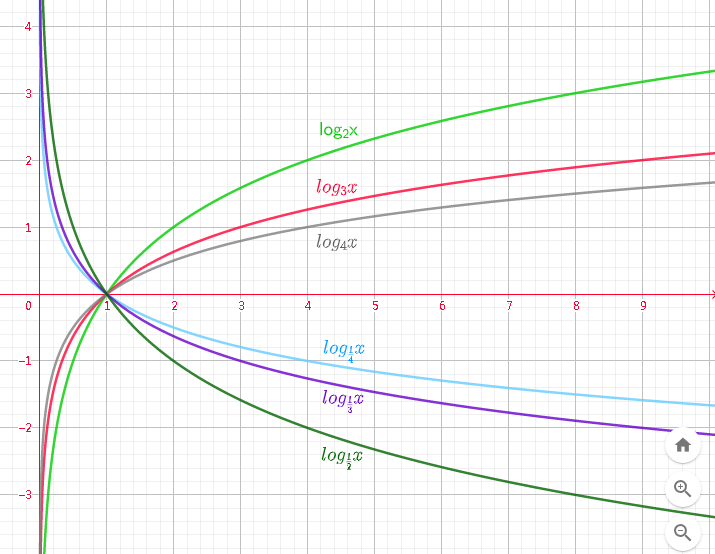
- 一般地,对数函数的图象和性质如下表:
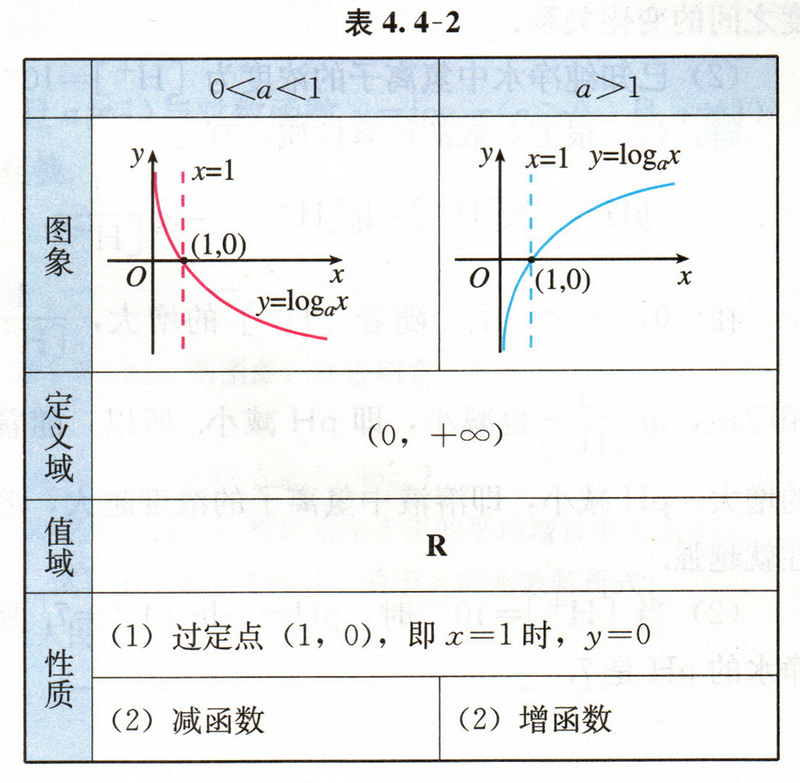
- 反函数(inverse function):一般地,指数函数 $y=a^{x}(a>0,且 a\neq 1)$ 与对数函数 $y=log_{a}x(a>0,且 a\neq 1)$ 互为反函数,它们的定义域与值域正好互换。
4.4.3 不同函数增长的差异
- 指数函数不像一次函数那样按同一速度增长,而是越来越快,呈爆炸式增长。
- 对数函数比较适合于描述增长速度平缓的变化规律。
4.5 函数的应用(二)
4.5.1 函数的零点与方程的解
- 对于一般函数 y=f(x),我们把使 f(x)= 0 的实数 x 叫做函数 y=f(x)的零点(zero point)。
函数 y=f(x)的零点就是方程 f(x)= 0 的实数解,也就是函数 y=f(x)的图象与 x 轴的公共点的横坐标。 - 函数零点存在定理:如果函数 y=f(x)在区间 $[a,b]$ 上的图象是一条连续不断的曲线,且有 f(a)f(b)< 0,那么,函数 y=f(x)在区间 (a,b)内至少有一个零点,
即存在 $c\in (a,b)$,使得 f(c)= 0,这个 c 也就是方程 f(x)= 0 的解。
4.5.2 用二分法求方程的近似解
- 二分法(bisection):对于在区间 $[a,b]$ 上图象连续不断且 f(a)f(b)< 0 的函数 y=f(x),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近视值的方法叫做~。
- 为了刻画与准确值的接近程度,这里给出了精确度 ε ,有 |a-b|<ε 可知,区间 $[a,b]$ 中任意一个值都是零点 $x_{0}$ 满足精确度 ε 的近视值。
4.5.3 函数模型的应用
- 数学建模活动
第五章 三角函数
5.1 任意角和弧度制
5.1.1 任意角
- 正角:我们规定,一条射线绕其端点按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有做任何旋转 - 任意角(ang angle):正角、负角和零角。
- 互为相反角:我们把射线绕端点按不同方向旋转相同的量所成的两个角叫做~。
- 第几象限角
- 所有与角 α 终边相同的角,连同角 α 在内,可构成一个集合 $S=\{\beta|\beta=\alpha+k\cdot 360°,k\in Z\}$,
即任一与角 α 终边相同的角,都可以表示成角 α 与整数个周角的和。
5.1.2 弧度制
- 角度制:用度作为单位来度量角的单位制
- 圆心角 α 所对的弧长与半径的比值,只与 α 的大小有关。
- 我们规定:长度等于半径长的圆弧所对的圆心角叫做 1 弧度(radian)的角,弧度单位用符号 rad 表示,读作弧度。
- 单位圆:半径为 1 的圆
- 正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是 0.
- 180° = π rad
1° = $\frac{π}{180}$ rad ≈ 0.01745 rad
1 rad = $(\frac{180}{π})°$ ≈ 57.30°
5.2 三角函数的概念
5.2.1 三角函数的概念
- 设 α 是一个任意角,$α\in R$,它的终边 OP 与单位圆相交于点 P(x,y):
(1)把点 P 的纵坐标 y 叫做 α 的正弦函数(sine function),记作 sin α,即 y = sin α;
(2)把点 P 的横坐标 x 叫做 α 的余弦函数(cosine function),记作 cos α,即 x= cos α;
(3)把点 P 的纵坐标与横坐标的比值 $\frac{y}{x}$ 叫做 α 的正切,记作 tan α,即 $\frac{y}{x}=tan \alpha(x\neq 0)$ - 三角函数(trigonometric function):正弦函数、余弦函数和正切函数(tangent function)的统称。
正弦函数 y = sin x,$x\in R$
余弦函数 y = cos x,$x\in R$
正切函数 y = tan x,$x\neq\frac{\pi}{2}+k\pi(k\in Z)$ - 终边相同的角的同一三角函数的值相等。
- 公式一:
sin(α + k·2π)= sin α
cos(α + k·2π)= cos α
tan(α + k·2π)= tan α,其中 $k\in Z$
5.2.2 同角三角函数的基本关系
- 同一个角 α 的正弦、余弦的平方和等于 1 ,商等于角 α 的正切。
$sin^{2}α+cos^{2}α=1$
$\frac{sin α}{cos α}=tan α (α\neq k\pi+\frac{\pi}{2},k\in Z )$
5.3 诱导公式
- 公式二(关于原点对称):
sin(π + α)= - sin α
cos(π + α)= - cos α
tan(π + α)= tan α - 公式三(关于 x 轴对称):
sin(-α)= - sin α
cos(-α)= cos α
tan(-α)= - tan α - 公式四(关于 y 轴对称):
sin(π - α)= sin α
cos(π - α)= - cos α
tan(π - α)= - tan α - 公式五(关于 y=x 对称):
$sin(\frac{\pi}{2}-α)=cos α$
$cos(\frac{\pi}{2}-α)=sin α$ - 公式六:
$sin(\frac{\pi}{2}+α)=cos α$
$cos(\frac{\pi}{2}+α)=-sin α$ - 公式一 ~ 公示六都叫做诱导公式(induction function)。
5.4 三角函数的图象与性质
5.4.1 正弦函数、余弦函数的图象
- 正弦函数的图象叫做正弦曲线(sine curve),是一条“波浪起伏”的连续光滑曲线。
- 余弦函数 y=cos x,$x\in R$ 的图象叫做余弦函数(cosine curve),它是与正弦函数具有相同形状的“波浪起伏”的连续光滑曲线。
5.4.2 正弦函数、余弦函数的性质
- 周期性
一般地,设函数 f(x)的定义域为 D,如果存在一个非零常数 T,使得对每一个 $x\in D$ 都有 $x+T\in D$,且 f(x+T)=f(x),那么函数 f(x)就叫做周期函数(periodic function)。非零常数 T 叫做这个函数的周期(period)。
周期函数的周期不止一个。
最小正周期(minimal positive period):如果在周期函数 f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做 f(x)的~。
正弦函数是周期函数,2kπ$(k\in Z 且 k\neq 0)$ 都是它的周期,最小正周期是 2π。
余弦函数也是周期函数,2kπ$(k\in Z 且 k\neq 0)$ 都是它的周期,最小正周期是 2π。 - 奇偶性
正弦曲线关于原点O对称,余弦曲线关于 y 轴对称。
正弦函数是奇函数,余弦函数是偶函数。 - 单调性
正弦函数在每一个闭区间 $[-\frac{\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi](k\in Z)$ 上都单调递增,其值从 -1 增大到 1;在每一个闭区间 $[\frac{\pi}{2}+2k\pi,\frac{3\pi}{2}+2k\pi](k\in Z)$ 上都单调递减,其值从 1 减小到 -1。
余弦函数在每一个闭区间 $[-\pi+2k\pi,2k\pi](k\in Z)$ 上都单调递增,其值从 -1 增大到 1;在每一个闭区间 $[2k\pi,\pi+2k\pi](k\in Z)$ 上都单调递减,其值从 1 减小到 -1。 - 最大值与最小值
正弦函数当且仅当 $x=2k\pi+\frac{\pi}{2},k\in Z$ 时取得最大值 1,当且仅当 $x=2k\pi+\frac{3\pi}{2},k\in Z$ 时取得最小值 -1;
余弦函数当且仅当 $x=2k\pi,k\in Z$ 时取得最大值 1,当且仅当 $x=2k\pi+\pi,k\in Z$ 时取得最小值 -1。
5.4.3 正切函数的性质与图象
- 周期性
正切函数是周期函数,周期是 π,即 $tan(x+\pi)=tan x,x\in R,且 x\neq\frac{\pi}{2}+k\pi,k\in Z$ - 奇偶性
正切函数是奇函数,即 $tan(-x)=-tan x,x\in R,且 x\neq\frac{\pi}{2}+k\pi,k\in Z$
正切曲线(tangent curve)是被与 y 轴平行的一系列直线 $x=\frac{\pi}{2}+k\pi,k\in Z$ 所隔开的无穷多支形状相同的曲线组成的。 - 单调性
正切函数在每一个区间 $(-\frac{\pi}{2}+k\pi,\frac{\pi}{2}+k\pi)(k\in Z)$ 上都单调递增。 - 值域
正切函数的值域是实数集 R。
5.5 三角恒等变换
5.5.1 两角和与差的正弦、余弦和正切公式
- 两角差的余弦公式:对于任意角 α,β 有
$cos(\alpha-\beta)=cos\alpha cos\beta + sin\alpha sin\beta$,称为差角的余弦公式,简记做 $C_{(\alpha-\beta)}$ - 两角和与差的正弦、余弦、正切公式(和角公式、差角公式)
$cos(\alpha+\beta)=cos\alpha cos\beta - sin\alpha sin\beta$,简记做 $C_{(\alpha+\beta)}$
$sin(\alpha+\beta)=sin\alpha cos\beta + cos\alpha sin\beta$,简记做 $S_{(\alpha+\beta)}$
$sin(\alpha-\beta)=sin\alpha cos\beta - cos\alpha sin\beta$,简记做 $S_{(\alpha-\beta)}$
$tan(\alpha+\beta)=\frac{tan\alpha+tan\beta}{1-tan\alpha tan\beta }$,简记做 $T_{(\alpha+\beta)}$
$tan(\alpha-\beta)=\frac{tan\alpha-tan\beta}{1+tan\alpha tan\beta }$,简记做 $T_{(\alpha-\beta)}$ - 二倍角的正弦、余弦、正切公式 (倍角公式)
$sin2\alpha=2sin\alpha cos\alpha$
$cos2\alpha=cos^{2}\alpha-sin^{2}\alpha$
$tan2\alpha=\frac{2tan\alpha}{1-tan^{2}\alpha}$
$cos2\alpha=1-2sin^{2}\alpha$
$cos2\alpha=2cos^{2}\alpha-1$
5.5.2 简单的三角恒等变换
5.6 函数 y=Asin(ωx+φ)
5.6.1 匀速圆周运动的数学模型
5.6.2 函数 y=Asin(ωx+φ)的图象
- 探索 φ 对 y=sin(x+φ)图象的影响
一般地,当动点 M 的起始位置 Q 所对应的角为 φ 时,对应的函数是 y=sin(x+φ)(φ≠0),把正弦曲线上的所有点向左(当 φ>0 时)或向右(当 φ<0 时)平移 |φ| 个单位长度,就得到函数 y=sin(x+φ)的图象。 - 探索 ω(ω>0)对 y=sin(ωx+φ)的图象的影响
一般地,函数 y=sin(ωx+φ)的周期是 $\frac{2\pi}{\omega}$,把 y=sin(x+φ)图象上所有点的横坐标缩短(当 ω>0 )或伸长(当 0<ω<1 时)到原来的 $\frac{1}{\omega}$ 倍(纵坐标不变),就得到 y=sin(ωx+φ)的图象。 - 探索 A(A>0)对 y=Asin(ωx+φ)的图象的影响
一般地,函数 y=Asin(ωx+φ)的图象,可以看作是把 y=sin(ωx+φ)的图象上所有点的纵坐标伸长(当 A>1 时)或缩短(当 0<A<1 时)到原来的 A 倍(横坐标不变)而得到,函数 y=Asin(ωx+φ)的值域是 $[-A,A]$,最大值是 A,最小值是 -A。
一般地,函数 y=Asin(ωx+φ)(A>0,ω>0)的图象,可以用下面的方法得到:
- 先画出函数 y=sin x 的图象;
- 再把正弦曲线向左(或右)平移 |φ| 个单位长度,得到函数 y=sin(x+φ)的图象;
- 然后把曲线上各点的横坐标变为原来的 $\frac{1}{\omega}$ 倍(纵坐标不变),得到 y=sin(ωx+φ)的图象;
- 最后把曲线上各点的纵坐标变为原来的 A 倍(横坐标不变),这时的曲线就是函数 y=Asin(ωx+φ)的图象。
5.7 三角函数的应用
- 弹簧振子、钟摆的摆动、水中浮标的上下浮动、琴弦的振动、交流电、温度变化、潮汐变化
- 简谐运动:在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为~。
- 在适当的直角坐标系下,简谐运动可以用函数 y=Asin(ωx+φ),$x\in[0,+\infty]$ 表示,其中 A>0,ω>0。
A 就是这个简谐运动的振幅,它是做简谐运动的物体离开平缓位置的最大距离;
这个简谐运动的周期是 $T=\frac{2\pi}{\omega}$,它是做简谐运动的物体往复运动一次所需要的时间;
这个简谐运动的频率由公式 $f=\frac{1}{T}=\frac{\omega}{2\pi}$ 给出,它是做简谐运动的物体在单位时间内往复运动的次数;
ωx+φ 称为相位;x=0 时的相位 φ 称为初相。