和孩子一起学“密铺”
今天周末,上午恩宝把作文写完,利用中午时间学点数学吧。他比较喜欢数学,家里有姐姐的数学课本,之前已经看过一遍,如今再重新学一回。
对于小孩子来说,重复对学习非常有必要,不要指望他能一下子全记住;还有一点就是要特别关注不要有曲解或记混淆的地方,错误的概念一旦形成,改起来就比较麻烦。对待语文也是这样,错误的读音、笔顺和错别字要及时发现与纠正。
更大方面来说,就是从小养成良好的学习、生活习惯,对以后的各项事情都有帮助。
上次课学的是“认识方程”,我们每次课都学一个单元,今天要学“数学好玩”。
第一个概念就是“`密铺”:
图形之间没有空隙,也不重叠,是密铺`。
问题1:
有一个房间,长宽分别是4.2米、3.6米,正方形瓷砖边长为0.5米,问能不能密铺?
恩宝的回答是不能,因为瓷砖到了边角需要裁切。
好吧,这是错误的理解,密铺的概念是没有限制面积的大小和形状的,它仅仅是指能不能把图形沿着四面八方拼成严丝合缝的形状。
为了简化问题,我们首先探讨了正多边形的密铺问题,先从正三角形开始。
经过绘图发现,能不能密铺可以先观察图形是否能够围成一个周角,或者能否形成平行线。
如下图正三角形可以通过旋转180°、上下颠倒、左右连接形成一长条,再把每一条并排在一起就可以密铺成更大的形状。
正三角形的顶角是60°,一周角正好可以放置 6 个正三角形。
通过观察下图,4 个正三角形可以密铺成大一点的正三角形,按照这个道理,可以无限的形成更大的正三角形,所以正三角形是可以密铺的。
对于正四边形,也就是正方形来看,密铺是显而易见的,如下图所示。
正五边形的顶角 = (5-2)x 180° / 5 = 108°,围成一周只能放下去三个,而剩余 36° 是无法再用正五边形填充,所以做不到密铺。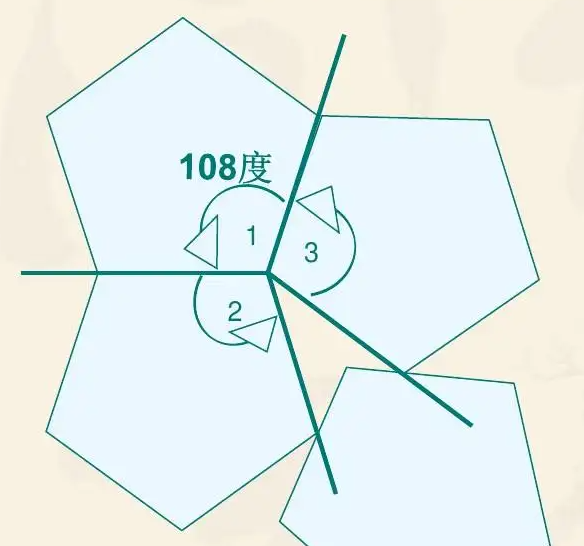
正六边形的情况就直观了,之前我们玩过的“昆虫棋”就是正六边形的,密铺显而易见。

那更多边形可不可以呢?
一个一个计算太麻烦了,还好之前已经教了恩宝 C++ 的 for 循环,直接编程实现吧。
#include <iostream>
using namespace std;
int main()
{
float angle; //正多边形的顶角
float angle2; //摆放之后的剩余角度
int num; //可以摆放正多边形的个数
for(float i=3;i<100;i++)
{
angle = (i-2)*180/i;
num =360/int((i-2)*180/i);
angle2 = 360 - num* angle;
cout<<i<<" : "<<angle<<" : "<<num<<" 个 "<<angle2<<endl;
}
return 0;
}计算结果如下:
3 : 60 : 6 个 04 : 90 : 4 个 0
5 : 108 : 3 个 366 : 120 : 3 个 0
7 : 128.571 : 2 个 102.857
8 : 135 : 2 个 90
9 : 140 : 2 个 80
10 : 144 : 2 个 72
11 : 147.273 : 2 个 65.4546
12 : 150 : 2 个 60
13 : 152.308 : 2 个 55.3846
14 : 154.286 : 2 个 51.4286
15 : 156 : 2 个 48
16 : 157.5 : 2 个 45
17 : 158.824 : 2 个 42.3529
18 : 160 : 2 个 40
19 : 161.053 : 2 个 37.8947
20 : 162 : 2 个 36
21 : 162.857 : 2 个 34.2857
22 : 163.636 : 2 个 32.7273
23 : 164.348 : 2 个 31.3044
24 : 165 : 2 个 30
25 : 165.6 : 2 个 28.8
26 : 166.154 : 2 个 27.6923
27 : 166.667 : 2 个 26.6667
28 : 167.143 : 2 个 25.7143
29 : 167.586 : 2 个 24.8276
30 : 168 : 2 个 24
31 : 168.387 : 2 个 23.2258
32 : 168.75 : 2 个 22.5
33 : 169.091 : 2 个 21.8182
34 : 169.412 : 2 个 21.1765
35 : 169.714 : 2 个 20.5714
36 : 170 : 2 个 20
37 : 170.27 : 2 个 19.4595
38 : 170.526 : 2 个 18.9474
39 : 170.769 : 2 个 18.4615
40 : 171 : 2 个 18
41 : 171.22 : 2 个 17.561
42 : 171.429 : 2 个 17.1429
43 : 171.628 : 2 个 16.7442
44 : 171.818 : 2 个 16.3636
45 : 172 : 2 个 16
46 : 172.174 : 2 个 15.6522
47 : 172.34 : 2 个 15.3192
48 : 172.5 : 2 个 15
49 : 172.653 : 2 个 14.6939
50 : 172.8 : 2 个 14.4
51 : 172.941 : 2 个 14.1176
52 : 173.077 : 2 个 13.8462
53 : 173.208 : 2 个 13.5849
54 : 173.333 : 2 个 13.3333
55 : 173.455 : 2 个 13.0909
56 : 173.571 : 2 个 12.8571
57 : 173.684 : 2 个 12.6316
58 : 173.793 : 2 个 12.4138
59 : 173.898 : 2 个 12.2034
60 : 174 : 2 个 12
61 : 174.098 : 2 个 11.8033
62 : 174.194 : 2 个 11.6129
63 : 174.286 : 2 个 11.4286
64 : 174.375 : 2 个 11.25
65 : 174.462 : 2 个 11.0769
66 : 174.545 : 2 个 10.9091
67 : 174.627 : 2 个 10.7463
68 : 174.706 : 2 个 10.5882
69 : 174.783 : 2 个 10.4348
70 : 174.857 : 2 个 10.2857
71 : 174.93 : 2 个 10.1408
72 : 175 : 2 个 10
73 : 175.068 : 2 个 9.86301
74 : 175.135 : 2 个 9.72974
75 : 175.2 : 2 个 9.60001
76 : 175.263 : 2 个 9.47369
77 : 175.325 : 2 个 9.35065
78 : 175.385 : 2 个 9.23077
79 : 175.443 : 2 个 9.11392
80 : 175.5 : 2 个 9
81 : 175.556 : 2 个 8.88889
82 : 175.61 : 2 个 8.78049
83 : 175.663 : 2 个 8.67471
84 : 175.714 : 2 个 8.57144
85 : 175.765 : 2 个 8.47058
86 : 175.814 : 2 个 8.3721
87 : 175.862 : 2 个 8.27585
88 : 175.909 : 2 个 8.18182
89 : 175.955 : 2 个 8.08987
90 : 176 : 2 个 8
91 : 176.044 : 2 个 7.91208
92 : 176.087 : 2 个 7.82608
93 : 176.129 : 2 个 7.74194
94 : 176.17 : 2 个 7.65958
95 : 176.211 : 2 个 7.57895
96 : 176.25 : 2 个 7.5
97 : 176.289 : 2 个 7.42267
98 : 176.327 : 2 个 7.34692
99 : 176.364 : 2 个 7.27274
从上面的数据中可以看出,正三角形、正四边形、正六边形可以围成周角。
正多边形顶角的变化
随着边数的增加,正多边形的顶角读数也不断增加,为了直观感受变化趋势,我们用Excel制作了折线图。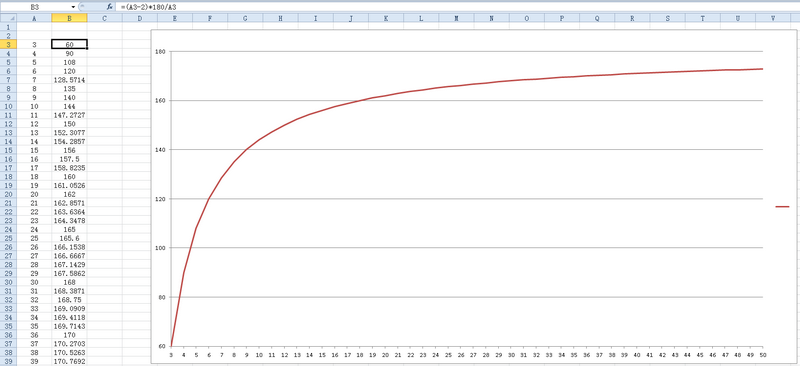
随着边数的增多,正多边形的顶角迅速向 180° 靠拢,但它会不会变成 180°,甚至超过 180°呢,这个问题恩宝经过思考也给出了正确的答案。
任意多边形的密铺
再返回头看一下任意多边形的密铺,还是依照从特殊到一般的原则来推理:
- 直角三角形:可以两两一组拼成长方形,可以密铺;
- 等腰三角形:可以通过旋转180°、上下颠倒、左右拼接形成平行四边形,可以密铺;
- 任意三角形:也可以通过旋转180°、上下颠倒、左右拼接形成平行四边形,可以密铺;
- 直角梯形:可以两两一组拼成长方形,可以密铺;
- 任意梯形:可以通过旋转180°、上下颠倒、左右拼接形成平行四边形,可以密铺;
- 任意平行四边形:左右、上下拼接,即可完成密铺。
上面的形状形成密铺都比较容易想象,那任意的四边形是否可以密铺呢,还是动手实验一下吧。
找来硬纸片,剪成任意四边形的样子,为了方便拼接,给每条边都编上号码,然后按照同边相接的原则开始沿着硬纸片的外缘画图,如下图所示:

可以看出四边形可以围绕一个点形成密铺,那会不会是因为绘制有误差造成的呢?
计算一下,四边形的内角和等于两个三角形的内角和,等于360°,那么绘图时依次选一个顶角对接,四个顶角正好可以围成一个周角,而且边依次衔接,如上图所示,按照这样的模式进行扩展就会发现任意四边形是可以密铺的。
再来看五边形的密铺,正五边形已经不行了,那其他的五边形呢?
五边形的内角和为540度,不能像之前四边形那样绕一个点旋转形成密铺,而且密铺时不但角度要能组合成周角,相接的边也要错落相等形成规律才可以实现密铺。
五边形密铺必定需要特殊形状,下面就是其中之一,把正六边形对半分形成五边形,即可实现密铺。
还有下面的密铺形状:
密铺还有多种图形组合形成的图案,这在日常的生活中很常见。
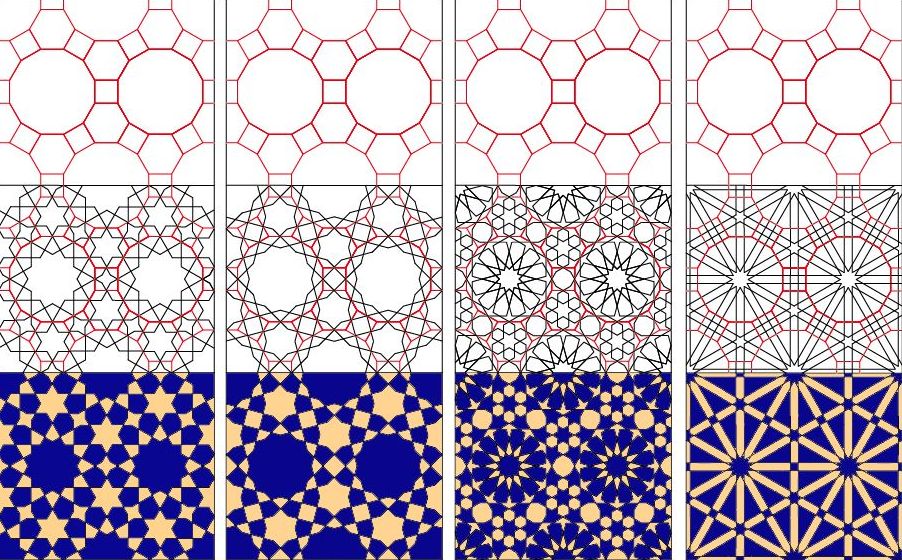
后记
前前后后居然讲了两三个小时,数学果然好玩。